Die Begrifflichkeiten
Es gibt Bücher und Artikel, die akribisch zwischen Kryptologie
und Kryptographie unterscheiden, andere verwenden diese Begriffe synonym. Dies ist auch
in dieser Arbeit der Fall, da durch die Unterscheidung der Begriffe
die Verständlichkeit und die Lesbarkeit nicht erhöht werden.
unterscheiden, andere verwenden diese Begriffe synonym. Dies ist auch
in dieser Arbeit der Fall, da durch die Unterscheidung der Begriffe
die Verständlichkeit und die Lesbarkeit nicht erhöht werden.
Ein Krypto-Verfahren oder auch Kryptosystem besteht aus einem Klartext,
dem zugehörigen verschlüsselten Text und den Schlüsseln
zum Chiffrieren und Dechiffrieren.
und Dechiffrieren.
Unter Kryptoanalyse versteht man den Vorgang, ein Krypto-Verfahren und
seine Kryptogramme zu untersuchen, so daß ohne die Kenntnis des Schlüssels der
Klartext erzeugt werden kann. Eine Methode, die bei der Kryptoanalyse
immer möglich ist, ist das sogenannte Brute-Force-Verfahren
zu untersuchen, so daß ohne die Kenntnis des Schlüssels der
Klartext erzeugt werden kann. Eine Methode, die bei der Kryptoanalyse
immer möglich ist, ist das sogenannte Brute-Force-Verfahren .
Allerdings besteht das Problem, daß dies nicht immer in angemessener
Zeit zu einem Ergebnis führt. .
Allerdings besteht das Problem, daß dies nicht immer in angemessener
Zeit zu einem Ergebnis führt.
Das Grundprinzip
Allgemein arbeiten alle Krypto-Verfahren nach dem gleichen Schema.
Dies ist in Abb.3.1.1 dargestellt.
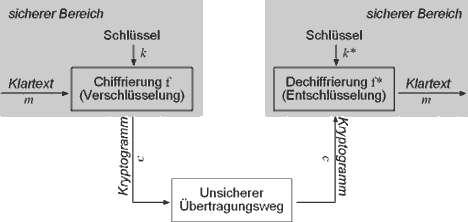 |
| Abb.3.1.1: allgemeines Kryptosystem |
Obige Abbildung.3.1.1 kann man auch mathematisch beschreiben. Das Kryptogramm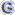 c wird durch eine Funktion f(k,m) erzeugt,
wobei k der Schlüssel (key) und m der Klartext
(message) ist. Die Funktion f(k,m)
ist also die Verschlüsselungsfunktion. c kann über
einen unsicheren Übertragungsweg übermittelt werden, ohne
daß jemand auf den Klartext schließen kann. Nur die Funktion
f*(k*,c) erzeugt wieder m.
c wird durch eine Funktion f(k,m) erzeugt,
wobei k der Schlüssel (key) und m der Klartext
(message) ist. Die Funktion f(k,m)
ist also die Verschlüsselungsfunktion. c kann über
einen unsicheren Übertragungsweg übermittelt werden, ohne
daß jemand auf den Klartext schließen kann. Nur die Funktion
f*(k*,c) erzeugt wieder m.
Das Aussehen der Funktionen f und f* und die Art der Schlüssel
k und k*legen die Ausprägung des Krypto-Verfahrens
fest.
Eine klassische Methode der Kryptographie
Kurze Beschreibung
Ein unter dem Namen CAESAR-Chiffre bekannt gewordenes Krypto-Verfahren,
das vom Namensgeber, dem römischen Imperator, benutzt worden sein
soll, ist wohl eins der einfachsten seiner Art. Es wird dabei das Alphabet
durch eins um k Buchstaben verschobenes ausgetauscht.
Ein Beispiel
Für k = 3 läßt sich folgende Tabelle zur
Verschlüsselung anlegen.
| A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
| ® |
® |
® |
|
|
|
|
|
® |
® |
® |
|
|
|
|
|
® |
® |
® |
|
|
|
|
|
|
|
| X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
So verschlüsselt sich m = "CDEF" zu c
= f(n,m) = "ZABC" oder
für m = "DAS WETTER WAR SCHOEN" zu c
= "AXP TBQQBO TXO PZELBK". Gerade der verschlüsselte
Text aus dem zweiten Beispiel läßt den Anschein zu, daß
das Kryptogramm wirklich die eigentliche Nachricht sicher verbirgt, doch bei genauerem
Hinsehen fallen schon Ähnlichkeiten von Klartext und Kryptogramm
wirklich die eigentliche Nachricht sicher verbirgt, doch bei genauerem
Hinsehen fallen schon Ähnlichkeiten von Klartext und Kryptogramm auf.
auf.
Denkbare Angriffsmöglichkeit
So bleiben die Wortlängen an sich erhalten, und gleiche Buchstabenfolgen
sind wieder zu erkennen, z.B. "ETTE" -> "BQQB".
Da eine natürliche Sprache gewisse Eigenarten hat, lassen sich
diese Kryptogramme schnell analysieren, so gibt es nur eine gewisse Zahl an Wörtern
mit drei Buchstaben, die häufig verwendet werden und auch einzelne
Buchstaben und Buchstabenkombinationen treten unterschiedlich häufig
auf. Der Buchstabe, der z.B. in der deutschen und englischen Sprache
am häufigsten Auftritt ist das "E"(s. relative
Häufigkeit von Buchstaben
schnell analysieren, so gibt es nur eine gewisse Zahl an Wörtern
mit drei Buchstaben, die häufig verwendet werden und auch einzelne
Buchstaben und Buchstabenkombinationen treten unterschiedlich häufig
auf. Der Buchstabe, der z.B. in der deutschen und englischen Sprache
am häufigsten Auftritt ist das "E"(s. relative
Häufigkeit von Buchstaben ).
So kann man für einzelne Zeichen und Zeichenkombinationen eine
Häufigkeitsanalyse durchführen und damit das Krypto-Verfahren
"knacken". Wenn nun dieses Wissen auf obiges Kryptogramm ).
So kann man für einzelne Zeichen und Zeichenkombinationen eine
Häufigkeitsanalyse durchführen und damit das Krypto-Verfahren
"knacken". Wenn nun dieses Wissen auf obiges Kryptogramm angewendet wird, stellt sich "B" als häufigster Buchstabe
heraus. Zwischen "E" und "B" liegt eine Verschiebung
von drei Buchstaben, damit gilt diese Verschiebung auch für jeden
anderen Buchstaben und so läßt sich der Klartext herstellen,
ohne daß der Schlüssel bekannt war.
angewendet wird, stellt sich "B" als häufigster Buchstabe
heraus. Zwischen "E" und "B" liegt eine Verschiebung
von drei Buchstaben, damit gilt diese Verschiebung auch für jeden
anderen Buchstaben und so läßt sich der Klartext herstellen,
ohne daß der Schlüssel bekannt war.
Es gibt viele Abwandlungen des CAESAR-Chiffres, aber alle lassen sich
mit recht geringem Aufwand lösen, gerade dann, wenn die Hilfe eines
Computers zur Verfügung steht. Dies gilt auch für alle anderen
monoalphabetischen Krypto-Verfahren, die mit Alphabeten natürlicher Sprache arbeiten.
Krypto-Verfahren, die mit Alphabeten natürlicher Sprache arbeiten.
Allerdings ist auf einen CAESAR-Chiffre natürlich auch genauso
ein Brute-Force-Angriff denkbar, denn bei 26 möglichen Schlüsseln ist es kein Problem,
für jeden eine Entschlüsselung zu berechnen und so den Klartext
zu gewinnen.
denkbar, denn bei 26 möglichen Schlüsseln ist es kein Problem,
für jeden eine Entschlüsselung zu berechnen und so den Klartext
zu gewinnen.
Der CAESAR-Chiffre zählt zu den symmetrischen ,
monoalphabetischen ,
monoalphabetischen Transpositions- oder auch Verschiebe-Chiffren.
Transpositions- oder auch Verschiebe-Chiffren.
Mathematische Darstellung
Als erstes sei jedem Buchstaben des Alphabets eine Zahl von 0 bis 25
zugeordnet, dann gilt für die Menge der zu verschlüsselnden
Zeichen M = {0,1,2,...,25} und eine ganze Zahl als Schlüssel
k folgende Funktion, die zeichenweise verschlüsselt:
| c = f(k, m) = (m + k) mod 26 |
Für die Entschlüsselung gilt dann die Umkehrfunktion:
| m = f*(k, c) = (c - k) mod 26 |
Die "mod n"-Schreibweise, bzw. ein Restklassenkörper
ist im Anhang A erklärt.
erklärt.
Weitere mono- und polyalphabetische Krypto-Verfahren sind in [BER94] zu finden.
zu finden.
Bewertung von Krypto-Verfahren
Zur Bewertung von Krypto-Verfahren werden im Wesentlichen zwei Kriterien
herangezogen. Zum einen die Sicherheit (die "Unknackbarkeit")
und zum anderen die Geschwindigkeit von Ver- und Entschlüsselung.
In [BER94] werden dazu drei Bedingungen aufgestellt, die ein Kryptoverfahren erfüllen
muß:
werden dazu drei Bedingungen aufgestellt, die ein Kryptoverfahren erfüllen
muß:
- Für jeden Schlüssel k und für jeden Klartext
m sind f(k, m) = c und f*(k,
c) = m leicht zu berechnen. D.h. die Ver- und Entschlüsselung
sollten bei bekanntem Schlüssel von einem entsprechnenden Computer
schnell ausgeführt werden.
- Für jeden Klartext m hat der chiffrierte Text c
= f(k, m) keine wesentlich größere Länge
als m selbst (damit die Übertragung der chiffrierten
Nachricht nicht erheblich länger dauert als die des Klartextes).
- Aus einem chiffrierten Text c kann ohne Kenntnis des
Schlüssels s nicht oder nur sehr schwer der zugehörige
Klartext m gewonnen werden.
Weiter sollte jedes Krypto-Verfahren mit seinen Implementierungen öffentlich
zugänglich sein, damit mögliche Fehler oder absichtlich einprogrammierte
Hintertüren erkannt und untersucht werden können. Das Ziel
ist hier nicht "security by obscurity". Ein Krypto-Verfahren
sollte seine Sicherheit nicht darauf aufbauen, daß die Algorithmen
nicht bekannt sind, sondern nur auf der Geheimhaltung des jeweiligen
Schlüssels. So ist es nämlich möglich, wenn dritten ein
Schlüssel bekannt wird, diesen einfach nicht mehr zu benutzen und
einen neuen zu wählen. Wenn allerdings ein geheimer Algorithmus
bekannt wird, so wird das ganze darauf beruhende Krypto-Verfahren hinfällig.
|