4.3 Die ECC-Parameter

In den letzten beiden Kapiteln sind die Kurvenparameter eingeführt und benutzt worden. Im weiteren sollen nun die gleichen Bezeichnungen gelten.

Die Ordnung r des Punktes G

Nach Gl.2.6.1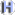 ist der Punkt G Generator einer Untergruppe U_G von E. In Kapitel 4.1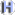 wurde für die Ordnung r des Punktes G, also für die Ordnung von U_G gefordert, daß diese eine Primzahl ist. Dies hat folgenden Grund: Bei der Schlüsselvereinbarung nach Kapitel 4.2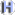 werden nämlich weitere Untergruppen von U_G erzeugt. Der öffentliche Schlüssel W ist ein Punkt der Gruppe U_G. W ist aber wieder Generator einer Untergruppe U_W der Gruppe . Aus der Gruppe U_W ist nämlich der gemeinsame Schlüssel k.
Nun ist die Ordnung #U_W dieser Untergruppe U_W ein Teiler der Ordnung r. Wenn r wie oben gefordert eine Primzahl ist, gilt also ggT(r, #U_W) = 1 oder ggT(r, #U_W) = r.
Was hat dies nun für die Kryptographie für Auswirkungen? Zum einen wird daraus deutlich, daß bei der Schlüsselgenerierung beachtet werden muß, daß W nicht eine Untergruppe mit der Ordnung 1 generiert, denn dann würde diese Untergruppe immer nur aus einem Punkt bestehen und zwar aus W, mit W = 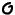. Da bei einer Multiplikation mit dem privaten Schlüssel s das Ergebnis auch immer W wäre und somit W auch der ausgetauschte in diesem Fall nicht geheime Schlüssel k, ist dieser Punkt W natürlich nicht für die Kryptographie geeignet.
Ähnliches wie für die Ordnung 1 gilt auch für die Ordnungen 2, 3, 4, ... . Das Ziel ist also, eine möglichst große Ordnung #U_W der durch W generierten Gruppe. Die maximale Ordnung #U_W ist aber die Ordnung von U_G, also r. Dies ist immer noch kein Grund warum r eine Primzahl sein muß, denn es wäre zur Bedingung zu machen, daß U_W die gleiche Ordnung wie U_G hat, dazu müßte dies aber beim Generieren des Schlüsselpaares überprüft werden, dazu ist es wiederum nötig, jeden Punkt aus U_W zu berechnen. Bei großen Gruppenordnungen ist dies aber sehr aufwendig. Weil aber die Schlüsselgenerierung u.U. sehr häufig ausgeführt wird, da die Schlüssel nur ein mal gültig sind, ist es das Ziel diesen Aufwand einzusparen. Dies geschieht mit der Bedingung, daß r eine Primzahl ist.

Die Ordnung r von U_G legt also die Anzahl der möglichen Ergebnisse des Schlüsseltausches fest. Somit ist die Größe von r ein wichtiger Faktor für die Sicherheit des Kryptosystems.

Im Weiteren folgen Bedingungen, die eine elliptische Kurve erfüllen muß, damit sie als kryptographisch stark bezeichnet werden kann, und somit für ein Kryptoverfahren basierend auf elliptischen Kurven geeignet ist. Diese Bedingungen verhindern, daß die Kurven spezielle Eigenschaften haben, so daß das Lösen des DLP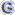 für diese Kurven vereinfacht werden kann.

Die Ordnung #E

Nach [PAU98]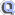 , S. 501f, muß für die hier betrachteten Kurven folgendes gelten.

• #E(Z_p) = r · c, wobei r > 2¹⁵⁰ eine Primzahl ist, c > 1 und ggT(r, c) = 1.
• (p)^l ¹ 1 mod r _{für 1 <= l <= 10 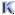Schützt vor Angriffen mit dem Subexponentiellen Index-Calculus-Algorithmen, die hier nicht behandelt werden.[PAU98]}

Wichtig ist hierbei, daß die Größenangaben für r und l im Moment (Oktober, 1999) als gültig betrachtet werden können, aber stark von der Entwicklung der Rechenleistung der aktuellen Computer abhängt und bei Implementierungen entsprechender Krypto-Verfahren darauf geachtet werden muß, daß diese Parameter bei Bedarf erhöht werden können..

Was bedeuten nun diese Bedingungen? Die Ordnung von E ist das Produkt einer großen Primzahl r und einer beliebigen Zahl c. Für den Punkt G war gefordert, daß dieser eine Untergruppe mit Ordnung einer Primzahl erzeugt, diese Ordnung ist r. Wie bekannt generiert, G eine Untergruppe von E, das bedeutet wiederum, und daß die Ordnung r von U_G die Ordnung #E teilen muß.

Die Bedingung r > 2¹⁵⁰ gibt an, daß r mindestens 150 geltende Bits hat. Da der private Schlüssel s zwischen 0 und r-1 liegt, gibt die Bedingung r > 2¹⁵⁰ auch die Schlüssellänge für s an. Die Schlüssellänge von W unterscheidet sich von der von s, da W aus einem Koordinatenpaar besteht, dessen Länge von p bestimmt wird.