|
Für die Kryptographie mit elliptischen Kurven wird, wie später
zu sehen ist, häufig das vielfache Addieren eines Punktes benötigt.
Daher folgt hier eine Beschreibung eines optimierten Verfahrens dieser
Addition und sei skalare Multiplikation genannt.
Unter der skalaren Multiplikation ist das n-fache Addieren eines Punktes
auf sich selbst zu verstehen, also P + P + .... + P + P,
dies wird als n · P oder kurz
nP geschrieben, wobei n in diesem Fall aus Z
ist.
Für große n ist die Berechnung von n ·
P sehr aufwendig, da jedesmal wieder die Steigung berechnet werden
muß, liegt es nahe, nach einem vereinfachten Verfahren zu suchen.
Beispiel für n = 25
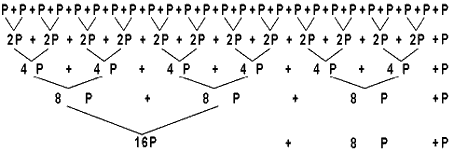 |
| Abb.2.5.1: 25 · P,
eine Vereinfachung |
Abbildung 2.5.1 zeigt, wie sich das Addieren der einzelnen Punkte in
mehrere Teilprobleme zerlegen läßt. Die Zerlegung in Teilprobleme
ist auf Grund der Assoziativität der Gruppe zulässig. So ist
in der zweiten Zeile nur noch 12 ·
(P+P) + P statt 24 mal P zu addieren. (P + P) kann
man mit einer Addition berechnen, d.h. es werden 24 - (12 +1 +1) = 10
Additionen eingespart. Die weiteren Zeilen folgen dem gleichen Schema,
denn wenn erst einmal (P + P) berechnet ist, dann ist das Ergebnis von
(P + P + P + P) nur eine Addition weit entfernt. Im Endeffekt werden
nur noch 7 Additionen benötigt, denn
| |
|
Benötigte Additionen: |
| 2P = |
P + P |
1 |
| 4P = |
(P + P) +( P + P) |
2 |
| 8P = |
(P + P + P + P) + (P + P + P + P) |
3 |
| 16P = |
(P + P + P + P + P + P + P + P) + (P + P + P + P + P + P + P +
P) |
4 |
Wobei natürlich bei der Berechnung von 16P alle vorherigen skalaren
Multiplikationen als "Abfallprodukt" mit berechnet werden.
Die Addition von 16P + 8P + P sind noch einmal zwei Additionen, also
sind es 2 + 4 = 6 statt 24 benötigte Additionen.
Bei genauerer Betrachtung erinnert oben Beschriebenes sehr an die Binärdarstellung
von Zahlen und wird verglichen; die Binärschreibweise für
25 ist 11001b. Analog dazu kann man obige Addition folgendermaßen
schreiben.
1 · 16P + 1 ·
8P + 0 · 4P + 0 ·
2 P+ 1· 1P = 25P
Für eine beliebiges n
Allgemein berechnet sich also das Produkt einer Zahl n Î
Z mit einem Punkt P folgendermaßen:
n schreibt sich in Binärdarstellung als [bz
bz-1
... b2
b1 b0].
Erst muß [bz 0 ... 0 0 0]P
berechnet werden, dazu sind genau z Additionen nötig. Danach läßt
sich dann
| n · P = |
|
bz ·
[ bz 0 ... 0 0 0]P |
|
| |
+ |
bz-1 ·
[0 bz-1 ... 0 0 0]P |
|
| |
+ |
... |
|
| |
+ |
b2 ·
[0 0 ... b2 0 0]P |
|
| |
+ |
b1 ·
[0 0 ... 0 b1 0]P |
|
| |
+ |
b0 ·
[0 0 ... 0 0 b0]P |
Gl.2.5.1
|
mit maximal z Addition berechnen. Also werden maximal
Additionen benötigt, wobei
| |
n » 2z
|
|
| Û |
z » log2
n
|
Gl.2.5.3 |
ist, das ist besonders für große n eine starke
Vereinfachung.
|